TriangleArray-CR3W

Dies soll keine Nachbauanleitung, kein wissenschaftlicher Bericht und keine Einführung in die Technik von „vertical arrays“ sein. Diesbezügliche Literatur findet sich bei ON4UN und an vielen Stellen im Internet. Hier soll lediglich eine Beschreibung und Zusammenfassung des von mir entworfenen Aufbaus des matching networks, den gewonnenen Erkenntnissen und Erfahrungen zum genannten Thema gemacht werden.

2. Motivation

Hintergrund der ganzen Aktion war der von mir seit langem gehegte Wunsch, einmal ein phasengespeistes array vollständig durch zu entwerfen und dann nach dem Aufbau die Ströme mit Phasen in den Elementen nachzumessen. Das Thema hat mich seit jeher interessiert, war jedoch bisher nicht umzusetzen. Die Platzverhältnisse meines qth’s sind leider nicht geeignet, derartige arrays aufzubauen.

Vor der diesjährigen Aktivität zum cqww rtty auf Madeira CR3W hatte Dieter, DK4QT, den Vorschlag gemacht, ein Vertical Triangular Array für 80m aufzubauen. Aus Platzgründen die Beschränkung auf drei Elemente und die Beschränkung auf drei Richtungen, um den Aufwand für die matching networks nicht zu hoch werden zu lassen. Der Azimut Öffnungswinkel ist zudem bei drei Elementen ziemlich groß, EZNEC gibt als 3dB-Öffnungswinkel den Wert Θ=130° aus.

Die Idee habe ich gern aufgenommen und da sie zeitig vor dem Contest kam, war auch genügend Zeit für die Vorbereitung. Schließlich musste fast das gesamte Material im Fluggepäck mitgenommen werden. Dieter DK4QT hat sich um die Masten mit Abspannungen, um die Koax Speiseleitungen und um das Steuerkabel für die Relais Umschaltung gekümmert.

Ziel des Experiments war für mich jetzt weniger, mit dieser Antenne die letzten qso’s für das Contest Endergebnis herauszuquetschen, sondern vielmehr, die Gelegenheit des Platzes zu nutzen, um Erfahrungen im Entwurf, Berechnung und Messung eines phased arrays zu sammeln.

3. Funktionsweise Arrays

Das Abstrahlungsdiagramm einer Richtantenne wird bekanntlich durch die Ströme und Phasen in den Elementen bestimmt. Während bei Richtantennen mit parasitär erregten Elementen die Verteilung der Ströme in den Elementen durch die Geometrie eingestellt wird, wird bei phasengespeisten arrays jedes Element mit einer eigenen Einspeisung versehen. Dadurch steigt die Anzahl der Freiheitsgrade bei der Auswahl der Geometrie, als Nachteil muss man die Notwendigkeit eines Anpass- und Verteilungsnetzwerkes, im folgenden „matching network“ genannt, für die Speisung der Elemente in Kauf nehmen.

Die Werte für die Ströme bzw. Phasen in den einzelnen Elementen für das geplante triangular array nimmt man entweder aus Empfehlungen in der Literatur oder man konstruiert sich ein Diagramm mit Hilfe einer Antennen Simulation Software, wie z.B. mit EZNEC. ON4UN macht in seinem „Low-Band Dxing“ 2nd Edition im Kapitel 11 verschieden Vorschläge zur Strom- und Phasenverteilung und zu den Abmessungen der Dreiecksgrösse. Wir haben uns hier auf folgende Werte konzentriert:
SW:                        I = 1 A und ϕ = 0°
SE:                          I = 1 A und ϕ = 0°
N:                           I = 1.8 A und ϕ = -110°
Seitenlänge:      24 m, gleichseitiges Dreieck
Mit diesen Werten erzeugt EZNEC folgendes Horizontal- bzw. Vertikal-Diagramm. 3dB-Öffnungswinkel ist Θ=132,4°.

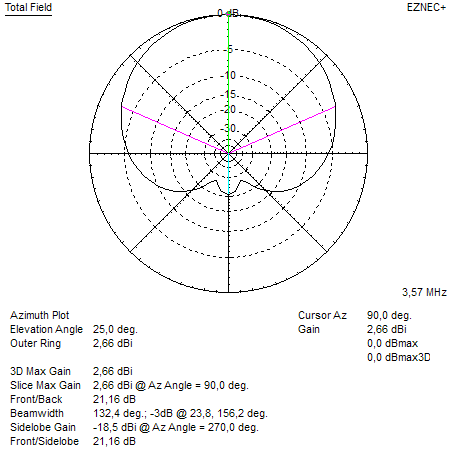
Abbildung 1: Azimutal Diagramm

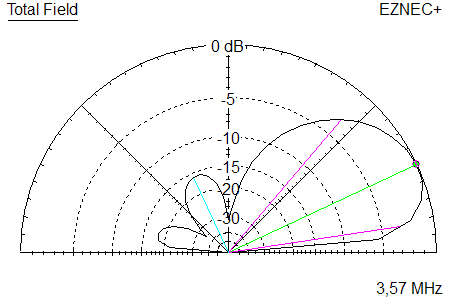
Abbildung 2: Vertikal Diagramm

Das array ist mit drei Elementen je 17m und einem Radialnetz von je 8 Radials à 12m Länge modelliert. Als Ground ist real/high accuracy mit den Standardwerten für die ground description verwendet. Die Radials befinden sich in diesem Model ca. 0,0012 λ über ground. Das ist deutlich weniger als der im EZNEC „user manual“ angegebene, empfohlene Wert.

Zitat „user manual”: “The minimum permissible height for horizontal wires depends on several factors, but results should be good down to at least 0.005 wavelength, or about 6 inches -- 15 cm -- at 10 MHz, or several wire diameters, whichever is higher.”

google: „Die minimal zulässige Höhe für horizontale Drähte hängt von mehreren Faktoren ab, aber die Ergebnisse sollten bis zu einer Wellenlänge von mindestens 0,005 oder etwa 15 cm (6 Zoll) bei 10 MHz oder mehreren Drahtdurchmessern, je nachdem, welcher Wert höher ist, gut sein.“

Bei dem bei mir eingesetzten, niedrigeren Wert ist die Übereinstimmung von gemessenen und simulierten Werten wesentlich besser als mit den bei EZNEC angegebenen. Vereinfacht gesagt, habe ich mit der Höhe der Radials über ground die Blindanteile der Fusspunkteimpedanzen der Realität angepasst.

Es ist nun ein matching network so zu entwerfen, dass sich später in den Elementen die Ströme und Phasenbeziehungen einstellen, wie sie oben angegeben sind.

Zudem sollte zum Abschluss des Experiments etwas folgen, was ich in der Literatur und im Internet noch nicht gefunden habe: nämlich die Nachmessung der Ströme in den Elementen nach Betrag und Phase. Nur so lässt sich überprüfen, ob das Anpassungsnetzwerk korrekt entworfen wurde und ob das array als Richtantenne funktioniert. Aus meiner Sicht sind Versuche, durch Umschaltung in verschiedene Richtungen mit S-Meter Vergleichen von verschiedenen Stationen nur behelfsmäßige Mittel, um die Funktion sicher zu überprüfen. Auch ein gutes SWR allein gibt keine Sicherheit.

4. Aufbau Elemente

Für den Aufbau der Elemente stand eine Grünfläche auf dem Grundstück des Hauses zur Verfügung. Die drei Spiderbeam Teleskopmasten wurden dort wie auf ABBILDUNG 3: ANORDNUNG DER 3 TELESKOPMASTEN aufgebaut. Die Anordnung Elemente war ein gleichseitiges Dreieck, Kantenlänge 24m.

Die Spitze des Dreiecks rechts oben zeigt mit einem Azimut von ca. 30° ungefähr in Richtung DL. NA liegt ca. Richtung NW, Südamerika liegt ca. in Richtung SO. Siehe auch ABBILDUNG 17: AZIMUT KARTE CR3W

Abbildung 3: Anordnung der 3 Teleskopmasten

Die drei Elemente wurden mit Spiderbeam 18m Fiberglasmasten aufgebaut. Diese Masten haben einen Durchmesser unten von 73mm und bestehen aus 12 Segmenten.

Die Strahler, je 18m Nyfaz Litze Ø1.5 mm, wurde ca. einmal pro Segment um den Mast geschlagen. Damit verkürzt sich die effektive Höhe des Strahlers auf ca. 17,6m. Die Masten wurden auf zwei Ebenen mit je drei Abspannungen 2mm geflochtener Kunststoffleine abgespannt, entsprechend der Empfehlung auf https://www.spiderbeam.com/product_info.php?info=p71_Spiderbeam%2018m%20fiberglass%20pole.html

Um den Aufbau selbst haben sich dankenswerterweise meine xyl Eleonore, Günter DL2AWG, Burkhard DF8XC, Ronny DM2RM, Jan DJ8NK, Thomas DL6TK und Dieter DK4QT gekümmert, so dass ich mich voll mit dem Aufbau der matching networks und den Messungen beschäftigen konnte.

Je ca. 8 Radials der Länge ca. 12m wurden auf dem Boden ausgelegt, wobei wg. des hohen Graswuchses die Drähte fast durchweg etliche Zentimeter Abstand zum eigentlichen Boden hatten. Als Draht wurde eloxierter Alu-Draht Ø1mm aus dem Gärtnereibedarf Bonsai verwendet. Geringes Gewicht und geringer Preis waren für die Anwendung an dieser Stelle prädestiniert.

Auf der Grünfläche unseres qth‘s sah das so aus:

Abbildung 4: Triangular Array

Vorne rechts ist der Mast N, im Hintergrund links ist SE und etwas verdeckt im Hintergrund rechts oben, an der Einfahrt zum Grundstück, ist der Mast SW zu erkennen.

5. Messungen für matching network layout

Die Messungen an den Elementen selbst wurden durchgeführt mit dem Vector Antenna Analyzer FA-VA4. Das Gerät ist batteriebetrieben, klein, handlich und eignet sich gut für kurze Messungen im Gelände.

Zunächst wurden jedem Elementen einzeln, ohne dass die jeweils beiden anderen Elemente aktiv waren, die Fußpunktimpedanzen gemessen:

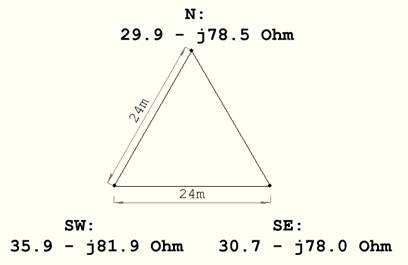
Abbildung 5: Messwerte Fusspunktimpedanzen

Von Interesse ist immer ein Vergleich zwischen den von EZNEC simulierten Werten für die Fusspunktimpedanzen und den vor Ort gemessenen Werten.

EZNEC	Messwerte Länge Strahler 18m Nyfaz 1.5mm²
je Element	SE	SW	N
34,03 - J 101,7 ohms ¹⁾	29.9 – j 78.5 Ohm	35.9 – j 81.9 Ohm	30.7 – j 78.0 Ohm

¹⁾ ein Mast hat 12 Segmente und der Strahler wurde einmal pro Segment um den Mast geschlagen. Diese Anordnung ist hier als Induktivität von 0,5 µH angesetzt und als Load in die Simulation EZNEC eingetragen worden. In der Größenordnung passt die EZNEC Simulation in etwa zu gemessenen Werten.

Es fällt auf, dass SE und N ungefähr gleiche Werte im Real- und Imaginärteil aufweisen, während SW in der Messung einen deutlich höheren Realteil aufweist, ca. 20% höher. Dieses Element stand am Grundstückseingang, oben rechts auf ABBILDUNG 4: TRIANGULAR ARRAY . Versuche, die Werte einander anzugleichen, wurden nicht unternommen.

Die Strahlerlängen sind für den geplanten Frequenzbereich zu kurz. Für die erforderliche Länge wäre eine Verlängerung mittels einer Dachkapazität möglich gewesen. Ich habe dennoch darauf verzichtet, um mögliche Längenkorrekturen und den damit verbundenen zeitlichen Aufwand für Abbau und Wiederaufrichten der Teleskopmasten zu vermeiden.

Um in den matching networks später an die Bauelemente weniger Anforderungen stellen zu müssen, wurde der Blindanteil der Fusspunktimpedanz mit Verlängerungsinduktivitäten kompensiert. Zur Vereinfachung und der damit verbundenen Zeitersparnis wurde hier in jedem Element eine kontinuierliche veränderbare Induktivität in Form eines Variometers verwendet. Dieses Variometer war von der Fa. Schubert GmbH bezogen in der einfachsten Bauform und vor Ort parallel geschaltet.
http://www.schubert-gehaeuse.de/variometer.html
Für einen stationären Betrieb würde man natürlich eine fest abgestimmte Induktivität verwenden.

Abbildung 6: Induktivität Strahler, Stromtrafo, Radials Anschlussleiste

Unten auf dem Foto ist das Anschlussstück für die Koax Speiseleitung, der Stromtrafo und die Klemmleiste für die Radials zu erkennen.

Vergleich zwischen EZNEC simulierten Werten und Messung vor Ort mit Induktivität:

EZNEC mit Induktivität 5,1µH	Messwerte Länge Strahler 18m Nyfaz 1.5mm² und Induktivität
je Element	SE	SW	N
34,53 + J 0,6071 ohms	35,8 + j 0,5 Ohm	43,1 + j 0,1 Ohm	36,9 + j 0,2 Ohm

Auch hier wieder die Feststellung, dass die Werte von Simulation und Messung relativ ähnlich sind. Auffällig ist auch hier der Ausreißer nach oben des Elements in SW (ca. 20%). Eine Erklärung dafür wurde nicht gefunden, s.o.. Möglicherweise war die unmittelbare Nähe zur Straße und damit das Fehlen des auf dem Rest der Grünfläche vorliegenden feuchten erdhaltigen Bodens die Ursache dafür. Die Elemente selbst waren jedenfalls alle gleich aufgebaut.

6. Berechnung drive impedances

Die Fusspunktimpedanzen der Einzelelemente sind also:
Z₁₁=35,8 + j 0,5 Ohm
Z₂₂=43,1 + j 0,1 Ohm
Z₃₃=36,9 + j 0,2 Ohm
Nach der Messung der Fusspunktimpedanzen der Einzelelemente werden die mutual impedances ermittelt. Diese können nicht gemessen werden, sondern müssen berechnet werden nach diesen Formeln:

Alle Berechnungen wurden mit Excel durchgeführt.

Z₁₂= 35,1 + j 4,3 Ohm
Z₁₃= 36,1 + j 7,3 Ohm

Z₂₁= 42,1 + j 4,7 Ohm
Z₂₃= 42,4 + j 6,4 Ohm

Z₃₁= 35,8 + j 5,9 Ohm
Z₃₂= 36,3 + j 5,1 Ohm

Z_xy sollte eigentlich gleich Z_yx sein; wo das nicht der Fall war, wurde der Mittelwert aus beiden Werten genommen.
Zusammen mit den Strömen und Phasen
I₁ = 1 A und ϕ = 0°
I₂ = 1 A und ϕ = 0°
I₃ = 1.8 A und ϕ = -110°
in den Elementen folgt die Berechnung der eigentlichen drive impedances mit diesen Beziehungen:

Die Berechnung der drive impedances ergibt:
Z₁ = 19,64 – j 19,3 Ohm
Z₂ = 29,03 – j 21,04 Ohm
Z₃ = 42,49 + j 15,31 Ohm
An diese drei berechneten drive impedances sind die Spannungen anzulegen, die die vorgesehenen Ströme in den Elementen erzeugen.

Dazu gibt es verschiedene Methoden, die z.B. in ON4UN „Low-Band Dxing 2nd Edition Vertical Arrays 11-3“ beschrieben sind. Ich habe mich hier für die Methode nach Gehrke K2BT entschieden, die bereits im Mai 1983 in der Zeitschrift „ham radio“ veröffentlicht worden war.

7. Übersicht Schaltplan Einspeisung

Die Koax-Speiseleitungen von jedem Element werden zur Mitte des Dreiecks Anordnung geführt und sind dort zunächst mit der Relaisbox zur Richtungsumschaltung und anschließend mit den matching networks verbunden, so dass letztlich eine Speiseleitung zur Station gelegt wird. Im Blockschaltbild sieht das so aus:

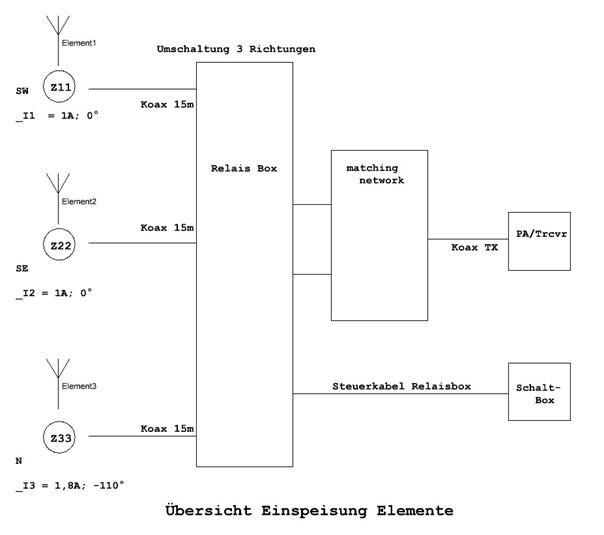
Abbildung 7: Übersicht Einspeisung

Je nach gewählter Richtung haben zwei Elemente haben immer gleiche Einspeisungswerte und werden in der Relaisbox parallelgeschaltet. Diese beiden parallelgeschalteten Elemente bilden den hinteren Teil und das verbleibende einzelne Element zeigt als vorderer Teil des Richtstrahlers in die Ausbreitungsrichtung.

8. Relaisbox und Umschaltung

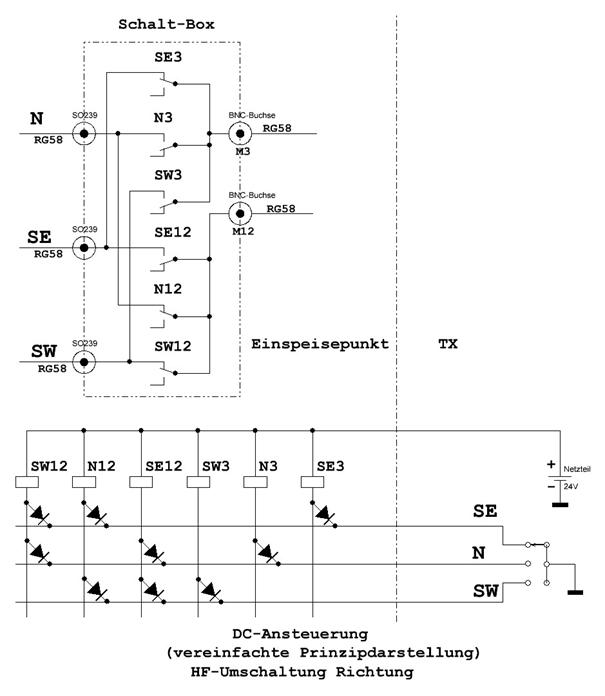
Abbildung 8: Relaisbox Umschaltung

Dies ist die Prinzipschaltung zur Umschalt Relaisbox. Wie bereits erwähnt, haben wir uns auf die Umschaltung in drei Richtungen beschränkt, da sonst ein komplettes zweites matching network erforderlich gewesen wäre. Für diese zusätzlichen Richtungen würden dann zwei Elemente parallelgeschaltet in die Hauptrichtung strahlen. Die Überlappung der Ausbreitungskeulen ist jedoch bei drei Richtungsschaltungen sehr breit und die Einbußen an Gewinn so gering, so dass sich der zusätzliche Aufwand nicht wirklich lohnen würde unter den gegebenen Umständen.

Das Shack ist etwa 50m Luftlinie entfernt vom Relais Umschaltbox an der Einspeisung des arrays. Die letztendlich benötigte Kabellänge konnte nur vor Ort ermittelt werden durch Auslegen des Kabels. Als Steuerkabel haben wir Ethernet kabel CAT5e eingesetzt und über Lüsterklemmen angeschlossen, um Steckeranschlüsse zu vermeiden. Die sonst üblichen RJ45 Stecker für dieses Kabel hätten vor Ort montiert werden müssen und das war mir zu riskant.

Wegen der geringen Kabelquerschnitte des CAT5e habe ich die Ansteuerung der Relais über Stromquellen vorgenommen. In den Zuführungen zu den Relais liegen in jeder Leitung zudem Leuchtdioden, sowohl auf der Schaltbox als auch in der Relaisbox. Damit war an beiden Boxen sofort zu erkennen, ob alle benötigten Relais angesteuert werden.

Abbildung 9: Schaltbox Relais im shack CR3W

9. Konzept Leistungsaufteilung

Das Konzept von Gehrke K2BT sieht vor, dass die Impedanz am Ausgang jeder Speiseleitung transformiert wird auf einen reellen Widerstand (also ohne Imaginärteil). Diese reellen Widerstände können dann ohne Phasenprobleme parallel zu den anderen geschaltet werden. Die Werte für diese (reellen) Widerstände berechnen sich aus den Leistungen, die im reellen Anteil der drive impedances am Fußpunkt der Antenne umgesetzt werden.

Gehrke K2BT berechnet also zunächst die Wirkleistungen, die in den einzelnen Elementen umgesetzt werden. Diesen Wirkleistungen ordnet er reelle Widerstände zu, die in der Parallelschaltung am Ausgang 50 Ohm ergeben. Am Beispiel des Triangular Arrays ergibt die Berechnung:

Element #	Wirkleistung	≙ Widerstand reell
SE	19,64 Watt	191,4 Ohm ²⁾
SW	29,03 Watt	191,4 Ohm ²⁾
N	137,66 Watt	67,7 Ohm
Gesamtleistung	186,33 Watt	Probe : 50 Ohm

Tabelle 3: Aufteilung Leistung

²⁾ die Koax Speiseleitungen von SE und SW werden am Eingang des matching networks parallel geschaltet und als ein Zweig behandelt. Im Idealfall wären die Leistungen in beiden Elementen gleich.

Hinweis: bei den o.g. Werten für die Leistung handelt es sich um reine Hilfsgrössen für die Berechnung der Komponenten des matching networks. Die Leistungswerte später im Betrieb weichen davon ab.

10.Koax Speiseleitung

Die Länge der Speiseleitungen kann bei dem von Gehrke K2BT verwendeten Verfahren frei gewählt werden. Die Längen können auch für die einzelnen Elemente unterschiedlich sein, was man aber zugunsten einer einfachen Umschaltung der Strahlungsrichtung tunlichst vermeidet.

Ausmessen der Speisekabel, RG58, Länge 15,6m, ergibt elektrische Länge @ 3,571 MHz (Frequenz ist willkürlich gewählt):
Kabel grau:         -99,79°                 Mantelwellensperre grau:          -4,95°
Kabel blau:         -99,79°                 Mantelwellensperre blau:          -4,89°
Kabel rot:            -99,77°                 Mantelwellensperre rot:             -4,73°

gemessen mit VNWA-3 von dg8saq. Die Messung der Schaltbox hat eine Länge von ca. 5° ergeben. Damit ergibt die elektrische Länge von ϕ=109,7° und die physikalische Länge der Speiseleitung ergibt sich bei einem Verkürzungsfaktor von v=0,66 zu len=16,9m.

Die (berechneten) drive impedances am Fußpunkt der drei Elemente werden durch die jeweiligen Koax Speiseleitungen transformiert. Die so transformierten Ausgangsimpedanzen kann man mit Leitungsgleichungen berechnen oder man berechnet sie mit Hilfe der Kettenmatrix. Hier bin ich dem Beispiel von Gehrke K2BT gefolgt und verwende Kettenmatrizen.

Die Kettenmatrix der driving impedanz Element SE lautet:

Z₁ =

Die Länge der Koax Speiseleitung inklusive der Länge in der Relaisbox mit Anschlusslängen habe ich bei der Frequenz 3,571MHz (qrg willkürlich gewählt) ausgemessen mit Θ = 109,7°, s.o.
Die Kettenmatrix einer verlustlosen Koaxleitung ist (allgemein, Z₀ = 50 Ohm):

Z_koax =

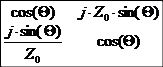
Die Matrix Multiplikation von Z₁*Z_koax = Z_in-koax ergibt:

Z₁ * Z_line =

Für den SE-Zweig ergibt sich dann am Ende der Koax Speiseleitung:
Z_in-SE = a11/a22 = 148,19 + j 10,95 Ohm,
Z_in-SW = a11/a22 = 100,67 + j 22,18 Ohm.
Z_in-N = a11/a22 = 40,16 - j 13,34 Ohm.

Im Rahmen der Vorbereitung habe ich an komplexen Widerständen mit ähnlichen Werten und einem RG58 Koaxkabel entsprechender Länge Kontrollmessungen gemacht und dabei abweichende Werte feststellen müssen. Die Erklärung dafür war, dass das Koax RG58 hier nicht als verlustlos behandelt werden darf. Bei RG213 hätten die Koax Verluste sicherlich vernachlässigt werden können. Das Kabel war aber zu schwer für den Transport.

Die Kettenmatrix für eine verlustbehaftete Leitung lautet:

Z_koax =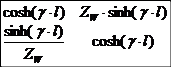

γ und Z_W sind komplexe Größen. Nun kann Excel zwar problemlos mit komplexen Zahlen rechnen, hat aber keine eingebauten hyperbolischen Funktionen für komplexe sinh bzw. cosh.

Diese müssen nach der Formel berechnet werden:

bzw.

und man erhält dann für die Impedanz am Kabeleingang:

Z_in-SE = a11/a22 = 131,35 + j 8,29 Ohm,
(zum Vergleich:
Z_in-SE = a11/a22 = 148,19 + j 10,95 Ohm
für verlustfreies Koaxkabel.)

Z_in-SW = a11/a22 = 94,11 + j 18,26 Ohm,

Z_in-N = a11/a22 = 41,17 - j 12,3 Ohm.

Das sind sichtbar andere Werte als mit verlustloser Koaxleitung.

γ enthält die Leitungsparameter für Widerstands-, Induktivitäts-, Ableitungs- und Kapazitätsbelag, angegeben in Ohm, Henry, Siemens und Farad pro Meter. Diese Materialangaben finden sich leider nur zum Teil in den Datenblättern der Hersteller. Anhaltswerte habe ich in der Software von AC6LA gefunden:

https://www.ac6la.com/tldetails1.html

Element	drive impedance	impedance Koax IN	zu transformierende impedance
SE	19,64 – j 19,3 Ohm	131,35 + j 8,27 Ohm	55,1 + j 7,6 Ohm¹⁾
SW	29,03 – j 21,04 Ohm	94,11 + j 18,26 Ohm	55,1 + j 7,6 Ohm¹⁾
N	42,49 + j 15,31 Ohm	41,17 – j 12,3 Ohm	41,17 – j 12,3 Ohm

Tabelle 2: Eingangsimpedanzen 3x Koax Speiseleitung

¹⁾ Koax SE und SW werden parallel geschaltet. Im Idealfall sollten diese beiden Werte gleich sein. Sie werden hier ohne weitere Maßnahmen parallelgeschaltet, die damit verbundenen Ungenauigkeiten werden hingenommen.

11.matching networks

Ich habe hier die klassische Vorgehensweise angewendet, wie sie Gehrke K2BT bereits im Jahre 1981 in seiner Artikelserie in der hamradio beschrieben hat. Die Methode funktioniert immer, setzt keine Spezialfälle voraus und sie war für mich in allen Punkten nachvollziehbar.

Für jedes Element gibt es dabei einen Einspeisungszweig. Alle Einspeisungszweige werden, vereinfacht ausgedrückt, an einer Stelle parallelgeschaltet und dieser Punkt wird dann als Antennenspeisepunkt mit dem Antennenanschluss des Transceivers verbunden. Das Problem ist natürlich dabei, die Aufteilung der TX-Leistung so auszulegen, dass sich die gewünschten Ströme in Amplitude und Phase in den Elementen selbst einstellen.

Die matching networks bestehen jeweils aus einem L-C-Glied, entweder mit shunt- oder mit serien-Element im Eingang. Die Formeln dazu können bei Gehrke K2BT oder bei ON4UN nachgesehen werden. Sie enthalten Terme mit Wurzelausdrücken, so dass es wg. der beiden Wurzel-Vorzeichen und des shunts- oder serien-Inputs maximal vier Varianten geben kann. Bei jedem der beiden matching networks. In der Regel gibt es nur zwei Lösungen pro matching network, abhängig davon, ob ein Transformationsweg unter den gegebenen Verhältnis möglich ist oder nicht. Von den gegebenen Möglichkeiten sucht man sich diejenige aus, die komponentenmässig am einfachsten zu realisieren ist.

12.matching networks hardware

Die Formeln zur zahlenmäßigen Berechnung der matching networks finden sich bei Gehrke K2BT und sind an dieser Stelle hier nicht abgebildet.

Mit den o.g. Werten am Ausgang der Koax Speiseleitungen habe ich diese Kombinationen gewählt:

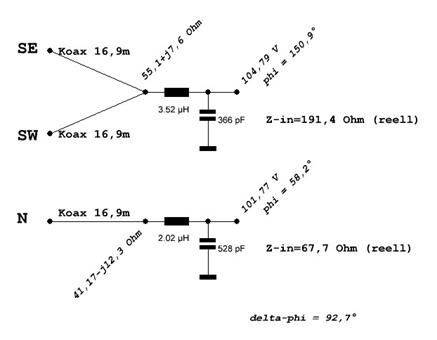
Abbildung 10: matching networks

Um vor Ort keine Zeit mit der Anpassung von Festinduktivitäten und Festkondensatoren zu verlieren, habe ich die beiden matching networks mit Rollspulen bzw. Drehkondensatoren aufgebaut und in einer spritzwassergeschützten Plastikbox untergebracht.

Abbildung 11: oben: Box = matching networks, unten: Box = line stretcher

Links im Bild ist die Relais Umschaltbox zu sehen.

Beide matching networks sind mit BNC Ein- und Ausgangsbuchsen versehen, so dass im Bedarfsfall zwischen shunt-input oder series-input gewechselt werden kann. Die Drehkondensatoren sind mit behelfsmäßig skalierten Einstellknöpfen ausgestattet. Bei den Rollspulen standen leider keine Antriebe mit Zählwerk zur Verfügung. Zur Einstellung der Induktivitäten bzw. Kapazitäten wurde folgendes Verfahren angewendet:

Die Drehkos wurden zunächst auf die berechneten Werte eingestellt. Die behelfsmäßige Skalierung ist dafür genau genug. Dann wurde auf der Seite des series-inputs ein Kurzschlussstecker auf die Buchse gesteckt und somit ein Parallel Schwingkreis provisorisch eingerichtet. Auf dem zweiten Anschluss, also an der Seite, auf der der shunt-Drehko lag, wurde der Netzwerkanalyzer VNWA-3e angeschlossen. Mit den Werten für L und C war die Resonanzfrequenz des Schwingkreises festgelegt und ließ sich beim Continuous Sweep des Analyzers beobachten. Mit der Rollspule wurde dann die gewünschte Resonanzfrequenz eingestellt.

Mittels Kettenmatrix Rechnung lassen sich die Spannungen an den Ausgängen der beiden matching networks berechnen:

U_SE-SW = 104,79 Volt
U_N = 101,77 Volt

Beide Werte sollten idealerweise gleich sein. Die Ursache für die Differenz ist darin zu suchen, dass bei der Aufteilung der Leistung in TABELLE 3: AUFTEILUNG LEISTUNG die durch die Kabeldämpfung verursachten Verluste in den Speiseleitungen nicht berücksichtigt wurden. Die Leistungen in beiden Zweigen sind unterschiedlich und damit auch die Spannungsabfälle verschieden. Aus Vereinfachungsgründen ist diese Ungenauigkeit ist hier nicht erfasst.

Die Phasen an diesen Stellen unterscheiden sich in der Regel. Das liegt daran, dass bei der Berechnung der matching networks nur Einfluss auf die Ausgangs-Impedanz genommen werden kann. Auf die Phasenverschiebung hat man keinen Einfluss bei der Berechnung.

13.line stretcher

Je nachdem welches Vorzeichen die Phasendifferenz besitzt, wird die Phase zu einem früheren (für ein positives) oder zu einem späteren (für ein negatives) Zeitpunkt Null.

Es muss also in einen der beiden Zweige ein Phasenglied implementiert werden, das das Δϕ = 92,7° an dieser Stelle auf null setzt. Gehrke K2BT nennt dieses Phasenglied „line stretcher“, in Analogie zu einer delay line mit reeller Source und reellem Abschluss, einzig zum Zweck, eine Phasenverschiebung zu implementieren. Ein solcher line stretcher wird mit diskreten Bauelementen aufgebaut und kann als pi- oder als T-Glied ausgeführt werden. Damit lässt sich ein Phasenvorlauf oder -nachlauf erzeugen.

Als Bezug für die Phasenverschiebung wird normalerweise der Zweig gewählt, in dem der line stretcher einen Phasennachlauf bewirken soll. Dann kann diese Komponente als pi-Glied mit einer Induktivität im Längszweig realisiert werden, was in der Praxis meistens am einfachsten zu realisieren ist.

Hier bietet sich an, eine Phasenverzögerung im Zweig N einzusetzen. Zum einen ist dieser Zweig niederohmiger und zum anderen ist in diesem Zweig ein Phasennachlauf erforderlich ist.

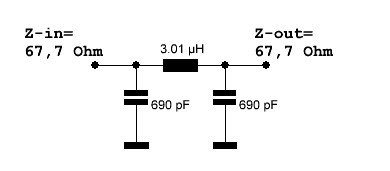
Abbildung 12: realisierter line stretcher

Die Simulation in RFSim99 zeigt, dass Phasenverschiebung mit dieser Schaltung erzeugt werden kann.

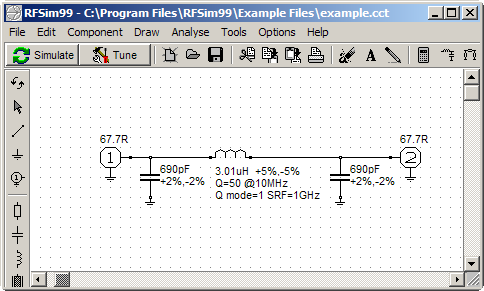
Abbildung 13: RFSim99 Schaltplan line stretcher

blau: -93,8Deg.

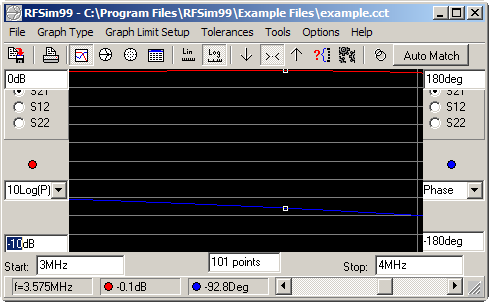
Abbildung 14: RFSim99 Phasenverschiebung

Die Einstellung der Werte erfolgt auch hier wie oben beschrieben. Nach Voreinstellung des Doppel-Drehkos auf den berechneten Wert wird auf einer Seite wird ein Kurzschlussstecker gesetzt und an die andere Seite der Analyzer angeschlossen. Mit der Rollspule wird die Resonanzfrequenz eingestellt.

14.Gesamtschaltbild matching network

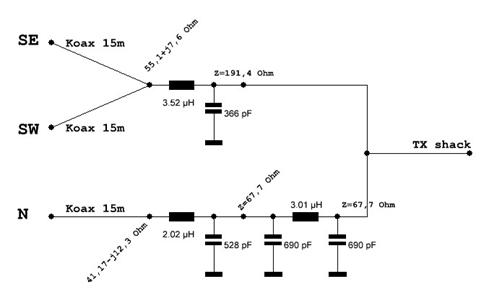
Abbildung 15: Gesamtschaltbild matching

15.Elementstrom und Phasenmessung

Ein zentraler Punkt bei diesem Experiment war die Messung der Elementströme und Phasen nach dem Aufbau zur Überprüfung der korrekten Arbeitsweise des arrays.

ON4UN gibt in seiner 2nd Edition „Low-Band Dxing“ auf Seite 11-17 im Kapitel 3.3.8 „Tuning and measuring vertical arrays“ ausführliche Hinweise zur Überprüfung der korrekten Funktion. Ich habe mich hier für die traditionelle Methode über Strommessung und Anzeige durch einen Mehrkanal Oszillografen entschieden. Eine andere Möglichkeit wäre, über einen im Ring geschalteten Multiplexer und einen Analyzer die Ströme nachzumessen. Ein geeigneter Multiplexer stand jedoch nicht zur Verfügung.

Um die Ströme messen zu können, muss erstmal ein Hf-Signal eingespeist werden. Zur Vermeidung von Fehlmessungen durch empfangene Signale und um nicht an die Empfindlichkeitsgrenze des Oszilloskops zu stoßen, sollte das Signal nicht zu schwach sein. Als Signalquelle habe ich den Analyzer VNWA-3e benutzt und dessen Ausgangssignal von ca. -17dBm mit einem Mini-Circuits RF Amplifier Typ ZHL-3A um ca. v=24dB verstärkt und damit auf etwa +7dBm Ausgangsleistung gebracht. Damit war ein problemloses Auslesen am Oszilloskop gegeben.

Zur Messung der Ströme wurden am untersten Teil eines jeden Strahlers ein Stromtrafo angebracht, siehe ABBILDUNG 6: INDUKTIVITÄT STRAHLER, STROMTRAFO, RADIALS ANSCHLUSSLEISTE.

Deren Sekundärwicklungen sind über drei gleich lange Koaxleitungen an die drei Eingänge des Oszilloskops angeschlossen. Dazu habe ich ein PC Oscilloscop 100 MHz/4 CH 1 Gsa/s PeakTech 1330 verwendet.

Damit lassen sich die aufgenommenen Sinuskurven u.a. als *.xls-file auf der Festplatte abspeichern und können durch Excel direkt ausgewertet werden. Während das Abspeichern in den herkömmlichen Formaten damit reibungslos funktioniert, gestaltet sich, möglicherweise bedingt durch irgendwelche Lizenzbestimmungen, das Abspeichern im *.xls-Format etwas kryptisch, aber man gewöhnt sich dran.

Benötigt werden letztendlich die Werte für Amplitude und Phase der drei gemessenen Sinusfunktionen. Die Auswertung kann man manuell über Cursoreinstellung auf dem Bildschirm machen, benötigt aber jedesmal einige Zeit. Leider hat Excel bei der (XY)-Diagrammdarstellung keine Trendlinienoptionen für Sinuskurven vorgesehen, so dass man auch hier die Auswertung normalerweise händisch vornehmen müsste. Dann kann man aber gleich die Cursorfunktion auf dem Oszilloskop Bildschirm benutzen.

Um schneller zu einem Ergebnis zu kommen, hat sich als Ausweg die Auswertung der Messwerte über die Fourieranalyse angeboten. Diese ist einmal in den Excel-Optionen unter dem Punkt Add-Ins, Analyse-Funktionen zu aktivieren. Maximal sind 4096 Werte möglich und die Anzahl der Messwerte muss eine Potenz von 2 sein, was hier aber keine Einschränkung darstellt. Maximale record length des P1330 sind 5M samples, also mehr als ausreichend.

Ich habe mir dazu eine kleine VBA-Software geschrieben, die aus jeder der drei Messreihen 512 Messwerte nimmt und analysiert. Es hat sich herausgestellt, dass 512 Werte reichen. Als Ergebnis der Fourier Analyse erhält man ebenso viele Werte als komplexe Zahlen. Der erste Wert ist der Gleichanteil, hier nicht von Interesse. Der Rest teilt sich je zur Hälfte auf in positive und negative Frequenzen. In der Mitte wird die Nyquist Frequenz ausgegeben. Da hier nur eine Frequenz von Interesse ist und um Zeit zu sparen, sucht die Software bei mir aus den ersten hundert Werten den Maximalwert Amplitude (Realteil) und die zugehörige Phase (Imaginärteil) heraus.

Als erste Messung vor Ort habe ich folgendes Ergebnis erhalten.

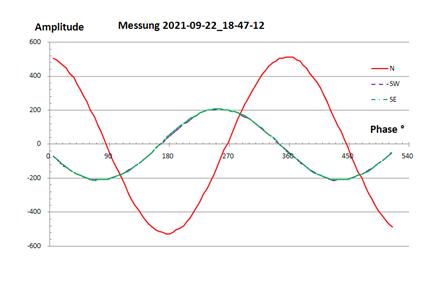
Abbildung 16: Ströme 1. Messung gleich nach dem Aufbau des arrays

Element	Amplitude	Phase
N	2,4	-101°
SW	1,0	0°
SE	1,0	-1°

Tabelle 4: Ströme 1. Messung nach Aufbau

Hier war zu sehen, dass die gemessenen Ströme und Phasen in den Elementen nicht so waren wie beabsichtigt. Das gemessene SWR am Eingang lag bei ca. SWR=1,55.

Es stellt sich nun die Frage, mit welchen Änderungen an den drei einstellbaren Induktivitäten und den drei Drehkos die optimalen Werte erreicht werden. Alle Änderungen wirken sich sowohl auf die Amplitude als auch auf die Phase aus, außerdem beeinflussen sie das SWR.

In der Vorbereitung zum Entwurf hatte ich nach einer Anleitung für eine systematische Vorgehensweise gesucht, jedoch nichts gefunden. So blieb vor Ort nur, versuchsweise vorsichtig an verschiedenen Einstellungen zu drehen und die Auswirkungen zu beobachten. Das Hauptaugenmerk lag dabei auf dem Erreichen der Elementströme und –phasen; das Eingangs SWR hatte nachrangige Priorität.

Nach etlichen Versuchen mit verschiedenen Einstellungen ergaben sich folgende Werte:

16.Ströme Richtung N

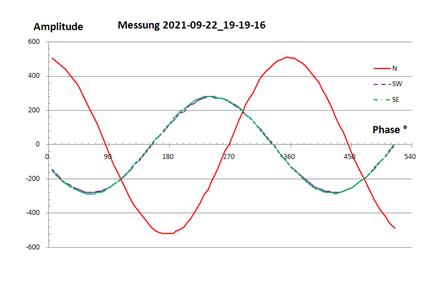
Abbildung 17: Ströme Richtung N

Element	Amplitude	Phase
N	1,8 A	-113°
SW	1,0 A	0°
SE	1,0 A	-1°

Tabelle 5: Ströme Richtung N

17.Ströme Richtung SE

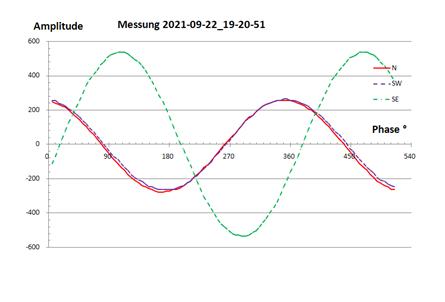
Abbildung 18: Ströme Richtung SE

Element	Amplitude	Phase
N	1,0 A	3°
SW	1,0 A	0°
SE	2,0 A	112°

Tabelle 6: Ströme Richtung SE

18.Ströme Richtung SW

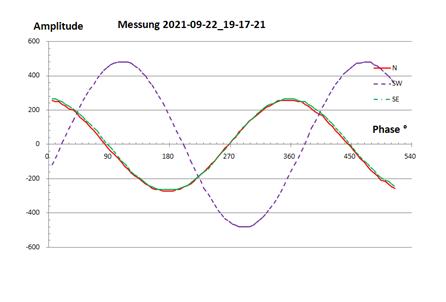
Abbildung 19: Ströme Richtung SW

Element	Amplitude	Phase
N	1,00 A	-1°
SW	1,82 A	-110°
SE	1,00 A	0°

Tabelle 7: Ströme Richtung SW

In allen drei Stellungen für die Strahlrichtung stellten sich also ungefähr gleiche Ströme und Phasen ein, so dass ich davon ausgehen konnte, dass die Richtungswirkung ok war.

Das SWR lag bei etwa 1,3 .. 1,4 und ich habe nicht versucht, durch Änderung der Einstellungen diesen Wert weiter zu drücken.

Nach wie vor kenne ich keine Strategie zur Optimierung der Einstellungen hin zu den gewünschten Strom- und Phasenwerten bei gleichzeitigem niedrigen SWR. Durch Nachjustieren an den Rollspulen und Drehkos der matching networks ist das Ziel erreicht worden, Ströme und Phasen wie geplant zu bekommen. Möglicherweise gewinnt man eine Übersicht über die Abhängigkeiten, wenn man in EZNEC für dieses array eine Simulation über alles einrichtet. Also entsprechend den Source Data etc. alle Teile des matching networks berechnet, diese dann in die Loads, Trans Lines und L Networks eingibt und anschließend systematisch die Abhängigkeiten für Ströme, Phasen und SWR dokumentiert. Dabei würde man auch die Auswirkungen auf die Richtcharakteristik mit einbeziehen, alles in allem also ein ziemlich umfangreiches Unterfangen mit zahlreichen Parametern.

Hier noch der Vollständigkeit halber die Auswertung Abschlussmessung des SWR:

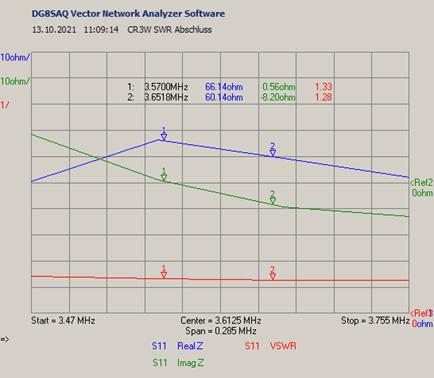
Abbildung 20: SWR Abschlussmessung

19.Betriebserfahrungen Triangle Array

Die Antenne wurde während des gesamten Contests cqww rtty an einer Station Flex 6000 mit nachgeschalteter PA ACOM-2000A betrieben. Ausgangsleistung war ca. 800 bis 1000 Watt. Davon dürften wg. des ca. 60m langen Koax RG213 etwa 700 bis 800 Watt an der Einspeisung angelangt sein. Ausfälle gab es nicht.

Für Ersatz- und Vergleichszwecke war eine zweite Antenne für 80m vorhanden, eine sloper am BP40 aufgehängt, schräg Richtung Norden.

Wie bereits in den Eingangsbemerkungen erwähnt, war es nicht das Ziel dieses Experiments, mit dem array die letzten qso’s aus den pile ups herauszuquetschen. Und für ausführliche Versuche, die Richtungswirkung des arrays zu testen, fehlte die Zeit.

Wg. der Beschränkung auf nur drei Richtungen war eine herkömmliche Überprüfung des Vor-/Rückverhältnisses, also durch Hin- und Herschalten von z.B. Nord-Süd, nicht möglich. Der 3dB-Öffnungswinkel ist lt. EZNEC Θ≈130°.

Einige wenige Umschaltversuche während des contests waren dennoch aufschlussreich. Die Versuche gelangen vor allem mit den lauten Stationen aus der Ukraine. Bei Stellung N zeigt das triangle array in die Himmels-Richtung Azimut 30°, also lt. Abbildung Richtung DL. Die Ukraine liegt im Azimut auf ca. 55°, was im Antennendiagramm einen Abfall von -0,44 dB gegenüber dem Maximum ausmacht.

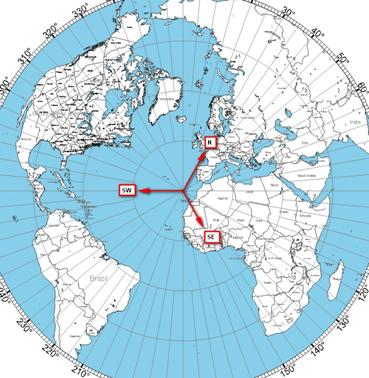
Abbildung 21: Azimut Karte CR3W

Bei Umschaltung auf SW (Antenne Azimut 270°) kommt UY (Ukraine) für die Antenne aus Richtung Azimut 55°. Im EZNEC Richtdiagramm befindet sich dieser Winkel im hinteren Teil der Ausbreitungsdiagramms, siehe Abbildung 13: Azimut Karte CR3W. Wg. der Aufzipfelung des Richtdiagramms in diesem Bereich ist es wenig sinnvoll, hier dB-Werte vergleichen zu wollen.

In dieser Stellung ging das S-Meter von z.B. vorher S9+10dB auf Werte jetzt ca. S8..S9 zurück. Im Mittel wurde ein Unterschied von ≈19dB abgeschätzt. Das entspricht in etwa der Charakteristik des EZNEC-Diagramms und kann als Indiz dafür gelten, dass das array die konzipierte Ausbreitungscharakteristik besessen hat.

Zwischen den Stellungen N und SE konnten bei der überwiegenden Anzahl der Stationen aus EU keine wirklichen Unterschiede ausgemacht werden. Dazu ist auch zu sagen, dass das qsb erheblich war und man für belastbare Aussagen längere Beobachtungsperioden bräuchte.

Leider habe ich in meinen Schichtzeiten keine Stationen aus dem südamerikanischem Raum oder der Karibik gesehen. Auch nicht aus Afrika, so dass diesbezüglich nichts zu berichten ist.

Beobachtung von Dieter DK4QT:

„OK, ich habe ja auf 80m damit gearbeitet und bemerkt, dass ich deutlich mehr Anrufe bekam, wenn ich vom Slooper auf die GP's geschaltet habe. RX hatte ich ja zum Teil die Beverage dran. Da habe ich nicht sodrauf geachtet. Richtung USA ging das Array besser!
Nun gut ... jedes Jahr das Array aufbauen ist wohl vom Aufwand übertrieben.“

Die Bezeichnungen für die Strahlungsrichtungen des arrays mögen etwas irritieren. Sie sind als Arbeitstitel in der ersten Phase des Entwurfs entstanden und am Aufstellungsort beibehalten worden.

Heye Harms, DJ9RR, im Oktober 2021.